Stateless Ethereum: Binary Tries Experiment

Originally published: https://medium.com/@mandrigin/stateless-ethereum-binary-tries-experiment

data & scripts for this article are in a github repo: https://github.com/mandrigin/ethereum-mainnet-bin-tries-data

What is Stateless Ethereum?

If you are already familiar with what Stateless Ethereum & Block Witnesses are, skip to the next part.

To run blocks and validate transaction, Ethereum nodes need to know the current state of the blockchain — all accounts & contracts balances and storages. This data is typically stored in the DB and is loaded into a Merkle trie when needed (to be able to verify hashes).

Stateless Ethereum clients work a bit differently. As the name implies, they don’t use a disk DB to run blocks (they might keep a full state though). Instead, they rely on block witnesses — a special piece of data, distributed together with a block, using which, a client can recreate a Merkle subtree, sufficient to execute all transactions inside the received block.

You can read more in depth about stateless clients in this article: https://blog.ethereum.org/2019/12/30/eth1x-files-state-of-stateless-ethereum/

Of course, distributing block witnesses means that the stateless nodes will use more traffic than regular nodes.

witness size chart (block 5.000.000–8.500.000)

There are a couple of ideas floating around on how to reduce the size of witnesses: using Validity / Computational Integrity Proofs (including but not limited to Zero-Knowledge), adding some compression, etc. One of the areas is switching Ethereum from hexary Merkle tries to the binary ones.

That is what this article is exploring. Let’s go.

Why Binary Tries?

One great property of Merkle tries is that you can validate the root hash even if you don’t have the full trie. In order to do that, every missing, but not empty path in the trie should be replaced with an appropriate hash value.

What is the problem with the hex tries?

Imagine that the full trie is filled with data (nodes have almost no nil children). To validate a single block we only need a relatively small percentage of nodes. So, we need to replace all the other paths with hashes to make this trie verifiable.

Each hash is something that adds more data to the block witness footprint.

If we switch to binary tries we can theoretically mitigate this issue because each node only has 2 children, so at most one of them will be replaced with a hash. (To paraphrase it, that means that we can “cut” the Merkle paths earlier, because our granularity is 1 bit instead of 4 bits in a hex trie).

That should cut the witness sizes significantly.

Let’s look at an example.

Imagine, that to run our block we only need one account: Acc1 with the path 3B (0011 1011). The tries are fully packed (nodes have no nilchildren).

Representations of the subtries that we need to be able to run our imaginary block are on the drawings below (in both hex and bin form).

The binary trie might look a bit more intimidating, but if that’s because I didn’t want to draw all the hash nodes in the hex trie.

So let’s count.

To produce a binary trie, the witness needs to contain 8 hashes, 7 branch nodes and 1 account node. That is 16 block witness elements.
To produce a hexary trie we need just one branch node, one account node and 15*2 = 30 hashes. That is 32 hash elements.

So, assuming that hashes and branches take the same amount of space in the block witness (they don’t, hashes are bigger), in our case the bin trie require a witness twice as small than the hex trie needs. Sounds cool.

That’s the theory.

Let’s see now how it works in practice. Let’s dive into the wilderness of the Ethereum mainnet.

Setting Up The Experiment

First things first: how do we validate if the produced block witness is usable?

To test that, we use the witness to produce a Merkle subtrie, run all the block’s transactions on it and validate the result. As long as all the transactions are executed successfully (there is enough gas, they have the same traces, etc), we can be sure that this witness is at least sufficient.

How we test (from https://github.com/ledgerwatch/turbo-geth/blob/master/cmd/state/stateless/stateless.go)

Secondly, we need some baseline data. For that, we got stats on the witness sizes using hex tries for the blocks 5.000.000–8.500.000 to compare and stored them in a gargantual csv file.

Our first attempt was to take a hex trie after a block is executed and convert it to a binary one just before extracting the witness from it.

This approach has some benefits: it is easier to implement, also it is trivial to validate that hex-to-bin conversion.

Unfortunately, we ran into two problems, one of them was critical.

First of all, as it turned out, hex tries contain more account nodes than similar binary tries. So, if we are converting them later, we don’t get the exact witnesses as it would be if we just had binary tries from the start.

Why is that?

That is due to a fact that hex tries always grow their height in 1/2 byte intervals. Bin tries grow in just 1 bit interval, that makes it possible to have tries with key length with odd number of bits.

In practice, there are some additional EXTENSION nodes in the witnesses and they are ever so slightly bigger. But even for big blocks (~5000 transactions) this difference was quite small comparing to the witness size (< 5%).

What was critical is the performance. With the growth of the trie, the conversion was slower and slower.

To put it in numbers, on our Google Compute Engine VM, the processing speed was around 0.16 block/second. That is less than 10 blocks per minute. To process 1.000.000 blocks we need more than 3 months. Oops.

So, we decided to go with a more complicated approach and built an experimental branch that uses binary tries natively. That means, that we replaced all hex tries in turbo-geth codebase with bin tries, so the blocks always run on binary tries.

On the downside, a few hashes checks had to be ignored (block root hash, and sometimes account storage hashes due to a limitation of our blockchain snapshots mechanism).

But the main verification mechanism stayed the same: we should be able to execute blocks using bin tries and subtries generated from witnesses.

Let’s talk about keys.

For simplicity, we encode keys very inefficiently: 1 byte per nibble; 1 byte per bit of a key. That simplified the code changes a lot, but the "keys” component of the block witness (see this article to learn what a witness consists of) is 8 times bigger than it should be, if we used bitsets (as we should).

So, for the further analysis I will assume that all keys are optimal (they encode 1 bit of information using 1 bit of memory).

Hex vs. Bin: Results

I ran the analysis on 2m blocks from the Ethereum mainnet in 2 intervals.

blocks 5.000.000–6.500.000

I will also provide commands to repeat the experiment using python scripts in the github repo: https://github.com/mandrigin/ethereum-mainnet-bin-tries-data

First, let’s analyze or dataset a bit.

python percentile.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust

a box plot, with the box between P25-P75 and whiskers between P1-P99

Percentile analysis (size in MB)

Now let’s make some cool charts!

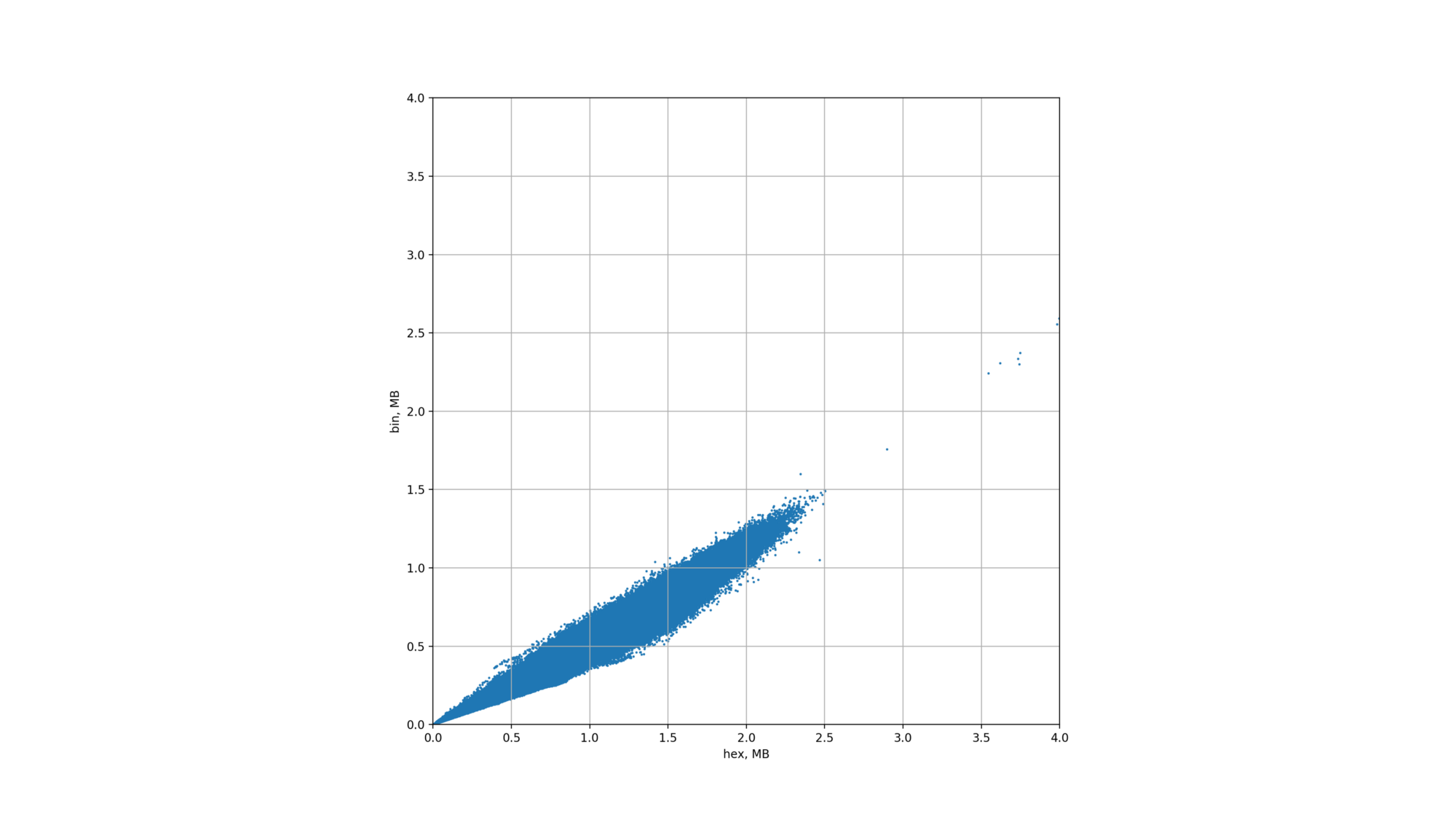
python xy-scatter-plot.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust

XY scatter-plot (adjusted for optimal keys)

As we see here, the size of binary witnesses is always better with binary tries.

Let’s plot another parameter, and divide our binary witness sizes to hex witness sizes to see what kind of improvement we can get.

python size-improvements-plot.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust

size of binary witness / size of hex witness (the smaller the better) across blocks

To understand this chart better, we can also print average, mean and percentile values like before.

mean = 0.51 = improvement 49%
p95 = 0.58 = improvement 42%
p99 = 0.61 = improvement 39%

What does it mean in practice?

For 99% of the blocks you will get at least 39% improvements in the witness size.
For 95% of the blocks you will get at least 42% improvements in the witness size.
On average, you will get 49% improvements of the witness size.

Let’s also see the absolute values of witnesses. To make them readable, let’s pick a sliding average of 1024 blocks.

python absolute-values-plot.py hex-witness-raw.csv bin-stats-5m-6.5m.csv 5000000 6500000 adjust

Witnesses sizes in MB across the timeline

Now, let’s repeat everything for the newer blocks.

blocks 8.000.000–8.500.000

python percentile.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust

Percentile analysis on blocks 8.000.000–8.500.000

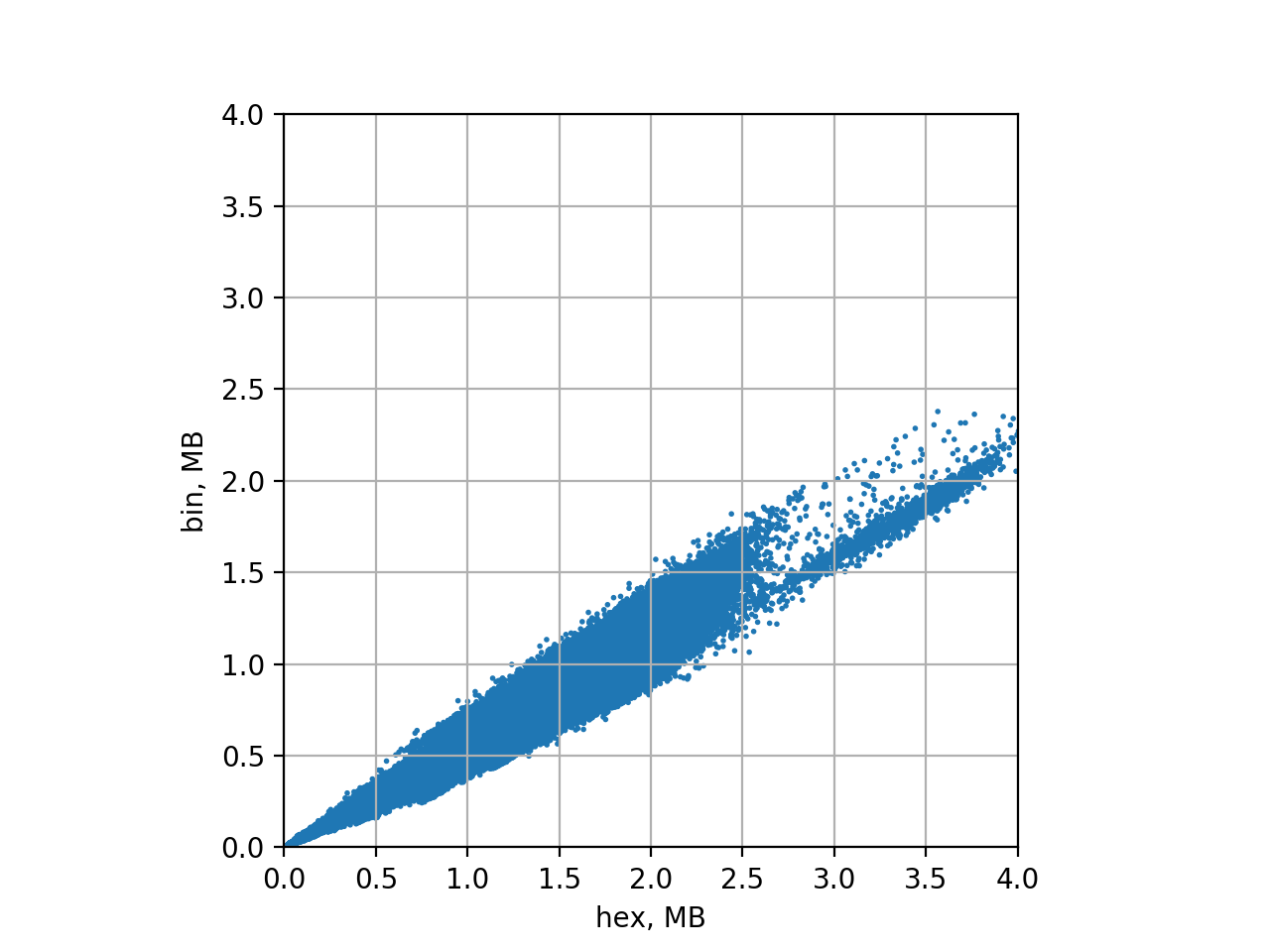
Now the XY scatter-plot

python xy-scatter-plot.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust

python size-improvements-plot.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust

mean = 0.53 = 47% improvements
p95 = 0.61 = 39% improvements
p99 = 0.66 = 34% improvements

And, finally, let’s plot witness sizes

python absolute-values-plot.py hex-witness-raw.csv bin-stats-8m-9m.csv 8000000 8500000 adjust

Conclusion

After running our tests on the real Ethereum mainnet data, we can see that indeed, switching to binary tries will give some significant improment for binary witness generation (bin witnesses are 47–49% smaller on average).

One more outcome is that this improvement isn’t as dramatic as the theoretical best case scenario. Possibly it is due to the real data layout in the mainnet blocks.

Probably, by analyzing some edge cases (where bin tries gave the least improvement) we can come up to more ways to improve block witnesses size.

Feel free to play with the raw data and scripts in the GitHub repo: https://github.com/mandrigin/ethereum-mainnet-bin-tries-data